💡 Stochastic RSI(스토캐스틱 RSI) 시그널로 시스템 트레이딩 구현하기
import pyupbit
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
먼저 stochastic rsi를 구하기 위해서는 rsi 값을 먼저 구해야한다.
def get_rsi(ohlcv, period):
ohlcv["close"] = ohlcv["close"]
delta = ohlcv["close"].diff()
up, down = delta.copy(), delta.copy()
up[up < 0] = 0
down[down > 0] = 0
_gain = up.ewm(com=(period - 1), min_periods=period).mean()
_loss = down.abs().ewm(com=(period - 1), min_periods=period).mean()
RS = _gain / _loss
return pd.Series(100 - (100 / (1 + RS)), name="RSI")
df['RSI'] = get_rsi(df, 14)
stochastic rsi를 구하는 함수는 아래와 같다.
def get_stochastic_rsi(data, k_window, d_window, window):
min_val = data.rolling(window=window, center=False).min()
max_val = data.rolling(window=window, center=False).max()
stoch = ( (data - min_val) / (max_val - min_val) ) * 100
K = stoch.rolling(window=k_window, center=False).mean()
D = K.rolling(window=d_window, center=False).mean()
return K, D
df['K'], df['D'] = get_stochastic_rsi(df['RSI'], 3, 3, 14)
stochastic rsi의 그래프를 보면 2개의 데이터로 이루어진다. get_stochastic_rsi 함수에서도 2개의 값을 반환한다. 실제 매매를 할 때 K 값을 사용하고 있으므로 K값을 활용하기로 결정했다. K값으로 그래프를 그리면 아래와 같다.

최종적으로 구하고자 했던 데이터는 고점이 내려가고 있는지 저점이 올라가고 있는지를 확인하는 것이다. 주어진 그래프에서는 고점을 내리고 있는 것을 확인할 수 있다.

고점과 저점을 구하기 위해서 변곡점을 구해야했다. 변곡점을 구하기 위해서 diff함수를 사용했다. diff 함수는 값들의 차이를 구하는 함수이다.
x = np.array([1, 2, 4, 7, 0])
np.diff(x) # array([ 1, 2, 3, -7])
diff의 결과를 보면 양수에서 음수로 전환되는 점이 고점이 되는 것을 확인할 수 있다.
# diff하여 나온 결과는 input array의 크기보다 1이 작다. 따라서 NaN 한 개를 추가하여 길이를 맞춘다.
df["diff"] = np.append([np.NaN], np.diff(df['K']))
def unit_cal(x):
if x != 0:
return x / abs(x)
else:
return 0
# 양수인지 음수인지만 활용하여 변곡점을 찾으므로 데이터의 크기를 상관없다.
# 따라서 -1, 0, 1로 변경하여 단순화한다.
df["unit"] = df["diff"].apply(unit_cal)
# 음수, 양수, 0을 구분하여 그래프에 표시한다.
fig, ax1 = plt.subplots(figsize=(15, 7))
ax1.plot(df['K'])
for idx, row in df.iterrows():
if row["unit"] < 0:
ax1.axvline(x=idx, color='red', linewidth=4.4, alpha =0.2)
elif row["unit"] > 0:
ax1.axvline(x=idx, color='blue', linewidth=4.4, alpha =0.2)
else:
ax1.axvline(x=idx, color='yellow', linewidth=4.4, alpha =0.2)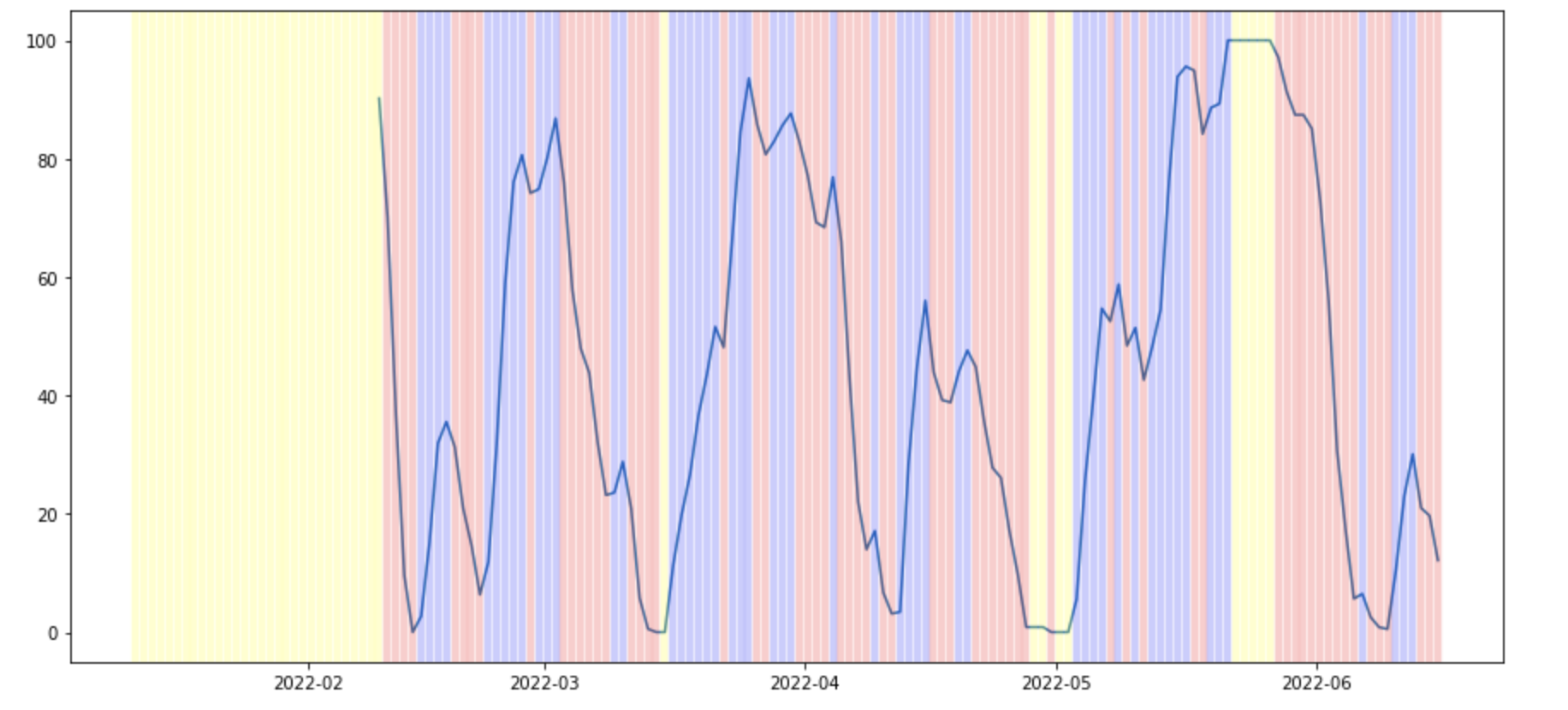
변곡점을 4가지(MAX, MIN, HIGH, LOW)로 분류하여 저장했다. MAX, MIN은
def inflection_classification(df):
df = df.copy()
df["shift_unit"] = df["unit"].shift(-1)
df["inflection"] = None
pre_inflection = None
for idx, row in df.iterrows():
# 이전 변곡점과 K값이 같은 경우 처리
if pre_inflection != None and row["unit"] == 0:
df.at[idx,"inflection"] = pre_inflection
else:
if row["K"] > 97:
df.at[idx,"inflection"] = "MAX"
elif row["K"] < 3:
df.at[idx,"inflection"] = "MIN"
elif row["shift_unit"] < row["unit"]:
df.at[idx,"inflection"] = "HIGH"
elif row["shift_unit"] > row["unit"]:
df.at[idx,"inflection"] = "LOW"
else:
df.at[idx,"inflection"] = None
pre_inflection = df.at[idx,"inflection"]
return df
classification_df = inflection_classification(df)
fig, ax1 = plt.subplots(figsize=(15, 7))
ax1.plot(classification_df['K'])
for idx, row in classification_df.iterrows():
if row["inflection"] == "MAX":
ax1.scatter(idx, row["K"], c="red")
elif row["inflection"] == "MIN":
ax1.scatter(idx, row["K"], c="orange")
elif row["inflection"] == "HIGH":
ax1.scatter(idx, row["K"], c="pink")
elif row["inflection"] == "LOW":
ax1.scatter(idx, row["K"], c="green")
elif row["inflection"] == "ZERO":
ax1.scatter(idx, row["K"], c="blue")
MIN과 MAX의 경우 얼마나 지속되었는지를 확인하기 위해 점의 개수를 counting한다.
def inflection_count_nesting(df, init_count = None):
df = df.copy()
if init_count != None:
df["count"] = init_count
pre_idx = None
for idx, row in df[~df["inflection"].isin([None])].iterrows():
if pre_idx != None:
current_inflection = row["inflection"]
pre_inflection = df.loc[pre_idx, "inflection"]
# diff값이 0인 경우 변곡이 생긴다. 아래의 code로 제거한다.
if (pre_inflection == "HIGH" and current_inflection in ["HIGH", "MAX"]) or (pre_inflection == "LOW" and current_inflection in ["MIN", "LOW"]):
df.at[pre_idx,"inflection"] = None
df.at[idx,"count"] = 1
# MIN, MAX가 연속적으로 발생하는 경우 count를 계산한다.
elif pre_inflection == current_inflection:
df.at[pre_idx,"inflection"] = None
df.at[idx,"count"] = df.loc[pre_idx, "count"] + df.at[idx,"count"]
pre_idx = idx
return df
count_nesting_df = inflection_count_nesting(classification_df, 1)
fig, ax1 = plt.subplots(figsize=(15, 7))
ax1.plot(count_nesting_df['K'])
for idx, row in count_nesting_df.iterrows():
if row["inflection"] == "MAX":
ax1.scatter(idx, row["K"], c="red")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "MIN":
ax1.scatter(idx, row["K"], c="orange")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "HIGH":
ax1.scatter(idx, row["K"], c="pink")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "LOW":
ax1.scatter(idx, row["K"], c="green")
ax1.text(idx, row["K"], row["count"])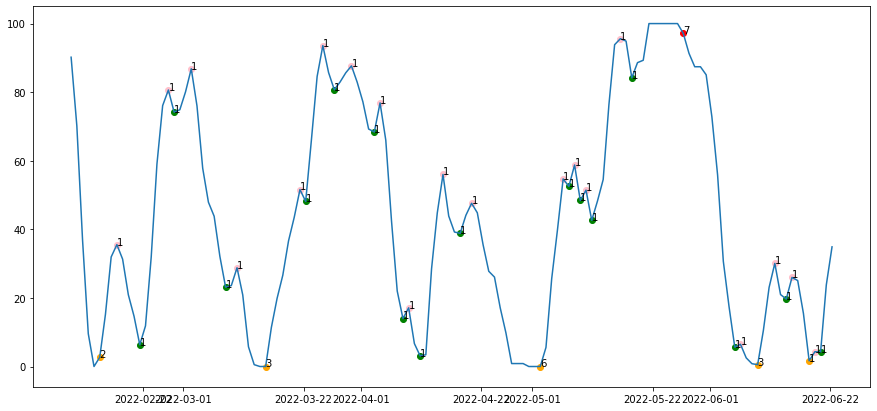
변곡점의 변동폭이 너무 작은 경우 무시해야하는 경우가 많다.
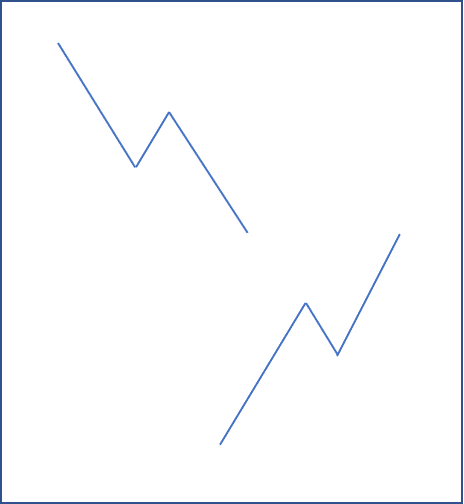

변곡점이 홀수개인 경우는 계속 상승하고 있는 경우이므로 제거한다. 변곡점이 홀수개인 경우는 전부 제거할 수는 없다. 가장 높거나 가장 낮은 변곡점만 남기고 제거한다.
def remove_inflection(df, inflection_list):
selected_inflection = None
last_inflection = inflection_list[-1]
inflections = list(map(lambda x: x[2], inflection_list))
# 변동폭이 작으면서 MAX, MIN이 포함되는 경우는 inflection을 MAX, MIN를 제외한 변곡점을 제거한다.
if "MAX" in inflections or "MIN" in inflections:
for inf in inflection_list:
if not inf[2] in ["MAX", "MIN"]:
df.at[inf[0],"inflection"] = None
df.at[inf[0],"count"] = 1
else:
# 변동폭이 작으면서 변곡점이 짝수인경우는 전부 제거한다.
if len(inflection_list) % 2 == 0:
for inf in inflection_list:
df.at[inf[0],"inflection"] = None
df.at[inf[0],"count"] = 1
# 변동폭이 작으면서 변곡점이 홀수인 경우는 가장 높거나 낮은 경우를 제외하고 전부 제거한다.
else:
if last_inflection[2] in ["MIN", "LOW"]:
min_inflection = reduce(lambda acc, cur: cur if acc[1] > cur[1] else acc, inflection_list, (0,101,0))
inflection_list.remove(min_inflection)
selected_inflection = min_inflection
else:
max_inflection = reduce(lambda acc, cur: cur if acc[1] <= cur[1] else acc, inflection_list, (0,-1,0))
inflection_list.remove(max_inflection)
selected_inflection = max_inflection
for inf in inflection_list:
df.at[inf[0],"inflection"] = None
df.at[inf[0],"count"] = 1
inflection_list.clear()
def flatten(df, k_diff):
df = df.copy()
pre_idx = None
inflection_list = []
for idx, row in df[~df["inflection"].isin([None])].iterrows():
if pre_idx != None:
current_inflection = (idx, df.loc[idx, "K"], df.loc[idx, "inflection"])
pre_inflection = (pre_idx, df.loc[pre_idx, "K"], df.loc[pre_idx, "inflection"])
# 변곡점의 변동폭이 k_diff보다 작은 경우 inflection_list에 추가한다.
if abs(current_inflection[1] - pre_inflection[1]) < k_diff:
if len(inflection_list) == 0 :
inflection_list.append(pre_inflection)
inflection_list.append(current_inflection)
# 변곡점의 변동폭이 k_diff보다 큰 경우가 발생하면 inflection_list에 추가되어 있는 변곡점을 제거한다.
else:
if len(inflection_list) > 1:
remove_inflection(df, inflection_list)
pre_idx = idx
if len(inflection_list) > 1:
remove_inflection(df, inflection_list)
return df
flatten_df = flatten(count_nesting_df, 7)
fig, ax1 = plt.subplots(figsize=(15, 7))
ax1.plot(flatten_df['K'])
for idx, row in flatten_df.iterrows():
if row["inflection"] == "MAX":
ax1.scatter(idx, row["K"], c="red")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "MIN":
ax1.scatter(idx, row["K"], c="orange")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "HIGH":
ax1.scatter(idx, row["K"], c="pink")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "LOW":
ax1.scatter(idx, row["K"], c="green")
ax1.text(idx, row["K"], row["count"])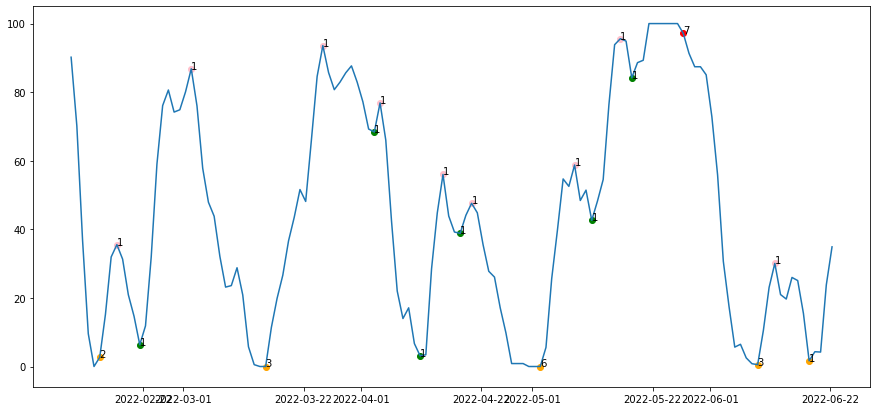
위의 코드를 정리하여 하나의 함수로 구현했다. flatten_diff는 변동폭이 작은 경우 제거하기 위핸 parameter이고 inflection range는 변곡점의 선을 그릴 때 변동폭이 너무 작거나 큰 경우를 제외시키기 위한 parameter이다.
def stockastic_rsi_analysis(df, flatten_diff, inflection_range):
df['RSI'] = GetRSI(df, 14)
df['K'], df['D'] = stochastic(df['RSI'], 3, 3, 14)
# diff하여 나온 결과는 input array의 크기보다 1이 작다. 따라서 NaN 한 개를 추가하여 길이를 맞춘다.
df["diff"] = np.append([np.NaN], np.diff(df['K']))
def unit_cal(x):
if x != 0:
return x / abs(x)
else:
return 0
df["unit"] = df["diff"].apply(unit_cal)
classification_df = inflection_classification(df)
count_nesting_df = inflection_count_nesting(classification_df, 1)
flatten_df = flatten(count_nesting_df, 7)
re_count_nesting_df = inflection_count_nesting(flatten_df)
fig, ax1 = plt.subplots(figsize=(15, 7))
ax1.plot(re_count_nesting_df['K'])
for idx, row in re_count_nesting_df.iterrows():
if row["inflection"] == "MAX":
ax1.scatter(idx, row["K"], c="red")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "MIN":
ax1.scatter(idx, row["K"], c="orange")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "HIGH":
ax1.scatter(idx, row["K"], c="pink")
ax1.text(idx, row["K"], row["count"])
elif row["inflection"] == "LOW":
ax1.scatter(idx, row["K"], c="green")
ax1.text(idx, row["K"], row["count"])
last_inflection_row = re_count_nesting_df[~re_count_nesting_df["inflection"].isin([None])].iloc[-1]
if last_inflection_row["inflection"] is "MIN":
second = re_count_nesting_df[re_count_nesting_df["inflection"].isin(["MIN", "LOW"])].iloc[-2]
if second["inflection"] is "MIN":
if last_inflection_row["count"] > second["count"]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return "짝궁"
if last_inflection_row["count"] == second["count"]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return "쌍궁"
else:
diff = last_inflection_row["K"] - second["K"]
if inflection_range[0] <= diff and diff <= inflection_range[1]:
return "짝궁"
if last_inflection_row["inflection"] is "LOW":
second = re_count_nesting_df[re_count_nesting_df["inflection"].isin(["MIN", "LOW"])].iloc[-2]
diff = last_inflection_row["K"] - second["K"]
if inflection_range[0] <= diff and diff <= inflection_range[1]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return "짝궁"
if last_inflection_row["inflection"] is "MAX":
second = re_count_nesting_df[re_count_nesting_df["inflection"].isin(["MAX", "HIGH"])].iloc[-2]
if second["inflection"] is "MAX":
if last_inflection_row["count"] < second["count"]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return("짝두")
if last_inflection_row["count"] == second["count"]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return "쌍두"
else:
diff = second["K"] - last_inflection_row["K"]
if inflection_range[0] <= diff and diff <= inflection_range[1]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return "짝두"
if last_inflection_row["inflection"] is "HIGH":
second = re_count_nesting_df[re_count_nesting_df["inflection"].isin(["MAX", "HIGH"])].iloc[-2]
diff = second["K"] - last_inflection_row["K"]
if inflection_range[0] <= diff and diff <= inflection_range[1]:
ax1.plot([second.name, last_inflection_row.name], [second["K"], last_inflection_row["K"]])
return "짝두"
df = pyupbit.get_ohlcv("KRW-KNC", interval="day")
print(stockastic_rsi_analysis(df,7,(5, 60)))
짝궁 신호가 발생한 것을 알 수 있다.
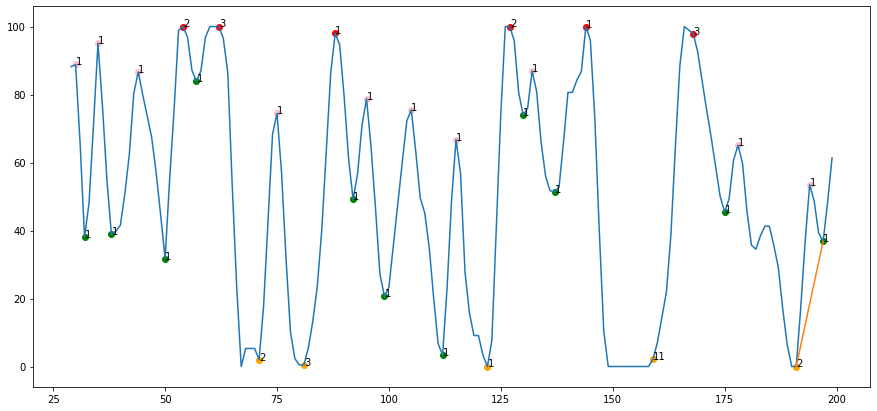
stochstic rsi 활용해 시그널을 구해보았다. 실제로 매매를 진행할 때는 stochstic rsi와 추세선을 함께 활용하고 있다. 다음에는 추세선을 그리는 방법에 대해서 알아보자.
'블록체인 > 블록체인이란?' 카테고리의 다른 글
| 공개 범위에 따른 블록체인. 퍼블릭 블록체인? 프라이빗 블록체인? 컨소시엄 블록체인? (0) | 2022.06.16 |
|---|---|
| 비트코인과 이더리움, 과연 뭐가 다를까? (1) | 2022.06.16 |
| 자료구조로써의 블록체인 (0) | 2022.06.16 |
| 기존 금융 시스템의 문제점, 신용 창출, 인플레이션 (0) | 2022.06.16 |
| [블록체인] 화폐의 역사, 화폐의 기능으로 본 암호화폐 (1) | 2022.06.16 |




댓글